2021年6月15日更新　投稿者 代表理事：澤　尚幸

数学をやれば神様が見えるようになる

――Salon De ∫u Ken流「数学学」――

「数学は得意ですか」と聞かれて「はい」と答えられる人はそれほど多くないでしょう。

難しい公式を覚えたり、証明問題を解いたりすることが何の役に立つのだろうと疑問に思う人もいるかもしれません。

では、なぜいま数学が重視され始めているのでしょうか。

大学時代は数学科に在籍していたという代表理事の澤が、デザイナーの川村貞知さん、建築家の古川泰司さんを相手に、“数学の気持ち”を解説します。

※本記事は動画「Salon De ∫u Ken #2『数学の気持ち』を語る by 澤尚幸」をテキスト化し、再編集したものです。

スピーカー紹介

「算数」と「数学」はどう違う？

古川：始まりました、「Salon De ∫u Ken」です。Community Future Designの澤尚幸さんは大学時代、数学科で数学を学んでいたそうです。そこで今日は「数学の気持ち」というテーマで話をしてもらおうと思います。それでは、さっそくバトンを渡しましょう。

澤：澤尚幸と申します。私は三重県の伊勢市で生まれました。みなさんも伊勢神宮は知っているかもしれませんね。神宮の建物は美しいなぁ、と思って育ちました。いつか読んだ本に、優秀な数学者が育ったところには美しいものがある、ということが書かれていて、妙に納得したことを思い出します。 実は数学では「ものの見方」が大事になってくるのではないかと私は考えています。ところで、今日の目標はこれです。

古川：いやいや、数学からいきなり「神様」が出てくるって（笑）。

澤：これはけっこう大事なんですよ。ただ、いきなり神様を見るのは難しいので、まずは神様の気持ちを知ることが数学では大切なのだという話をします。今日の話は島根県江津市の「GO▶つくる大学」という市民大学で行った講義がもとになっています。今から2年くらい前、「数学とは何かわかるような授業をしてほしい」と頼まれて、「数学学」という講座をやりました。その時、市民大学の企画の方から「神様の証明」という副題をいただいて、授業の内容をそれに合わせたんですね。目線を高くするのが数学です、という感じでしょうか。それでは、さっそく本題に入っていきましょう。みなさんは「算数」と「数学」の違いを知っていますかね。川村さんはわかります？

川村：小学生までが算数で、中学生から数学。習う時期の違いですか？

澤：まあ、それもあります。あとは字の違いですよね。「算」と「学」。

「算数」は英語で「calculation」です。「calc」は「石」という意味なんですよ。昔は数える時に石や木の枝を使っていたんです。要するに「数を数えること」が「算数」ですね。

「数学」は英語で「mathematics」で、古代ギリシアでは「μαθηματα（マテーマタ）」と言いました。これは「学ばれるべきもの」という意味の言葉で、国を治めるために必要な要素を指しました。数の役割を考える数（すう）論、天文学、幾何学、あと音楽も。つまり、数学よりももっと広いエリアの話だったんですね。

古代ギリシア以前はおそらく、感覚的に政治が行われていたのだと思います。そうではなくて思考しましょう、思考するためにも数と量をしっかり捉えましょう。それが「mathematics」のそもそもの意味です。ものの本を読むと「mathematics」を「数学」と訳した明治時代の人が駄目だったのではないかとも指摘されています。

古代ギリシア以降にも、完璧な宮廷を作るには数学者を入れないと駄目だと主張した皇帝がいるんですよ。女帝エカテリーナの逸話ですね。数を把握できる人が行政・政治の世界には必要だと。僕も数学科の人たちには「世の中に求められているから、もっと前に出てきてほしい」とよくお話しするんですよね。

川村：「mathematics」を「数学」と訳した明治時代の人が駄目だった――それは「ネーミングで失敗した」ということですかね？　数学をブランディングする時にしくじった。ネーミングが変われば、また見方が変わって、ハードルが下がるかもしれないですね。

澤：さすがデザイナー、いいこと言いますね。数学は1回わからなくなると、挫折感がすごい科目じゃないですか。嫌いだと聞くと寂しいんですよ。もうちょっと楽しい感じでブランディングできないですかね。

川村：「数」という漢字が駄目なのかなあ。この時間内で考えてみます。数学の新しいネーミングをね。

澤：素晴らしい、よろしくお願いします（笑）。話を戻すと、「数や量をもとに、ものごとをしっかり考えてみましょう」というのが数学で、計算に重きが置かれている算数とは少し違います。日本でも、ここ3年くらいで「エビデンス（証拠）に基づいて政策を決めましょう」と「EBPM（Evidence-based Policy Making）」が推進されるようになってきました。行政が感覚ではなく、数や量で捉えようとするようになってきたのは、すごくいいのかなと思います。最近話題になった安宅和人さんの『シン・ニホン』という本も、基本的にはエビデンスについて書かれた本ですよね。これは数学とつながっていると思います。

習っていることは「紀元前」の発見

澤：ところで、みなさんが算数や数学で学んでいることは、かなり古い時代に発見されているんですよ。

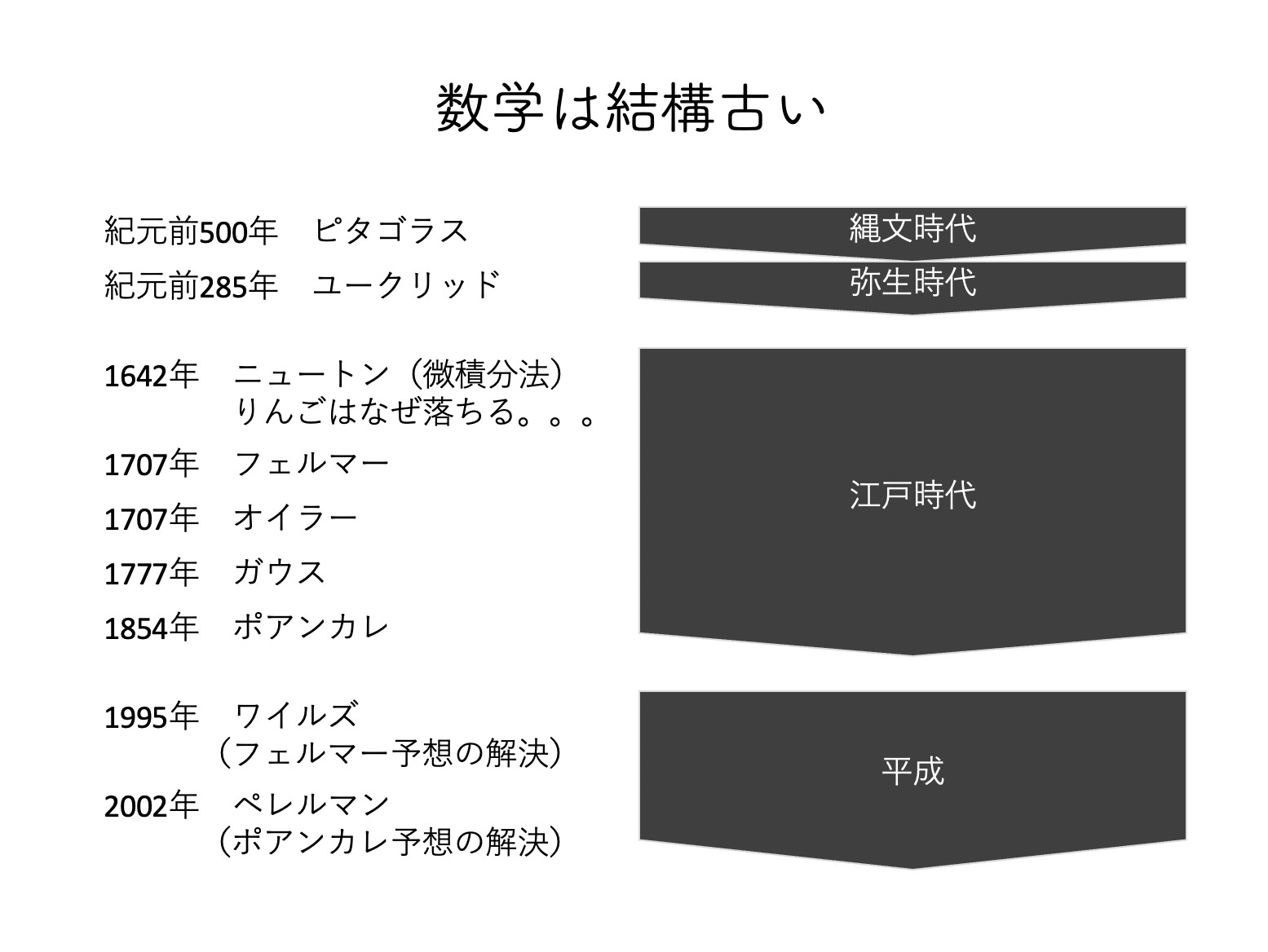
「ピタゴラスの定理」や「ユークリッド幾何学」なんて紀元前。微積分法ですら1642年で、日本で言えば江戸時代の前期です。その後に出てくるフェルマーやオイラー、ガウスは、それでも1700年代です。算数や数学で習っていることは、そうとう基礎的で、しかも古い。これも意外とみなさん、知らないのではないかと思います。

古川：やっぱりネーミングを考える時は、こういう情報も重要じゃないですかね。「僕らはこんなに古いことをやっているんだよ」と。

川村：脈々と続いている歴史があるわけですね。

澤：そこまで古いことを教えるのは、やっぱり必要だからだと思うんですよ。数学では一度何かが証明されたらそれが100％正しくて、後になって覆されることはまずありません。そこが哲学や他の学問とは違っているのかなと。だからこそ安心感があるし、ものを決めていく時の基準になりうる。そう捉えてもらうといいかもしれません。ちなみに、数学をやっている人には「本当にそうかな」や「なぜ」が口癖だという特徴があります。「答えはAだ」と思ったら「Aではない場合はどうなのか」と考えたくなってしまう。

川村：「常識を疑うところからスタートする」というのと、何か関係ありますかね？　みんなの思い込みを少しずらしてあげる。そこからアイデアが生まれる……。

澤：それは関係あるかもしれないですね。教育に関わっていると、みずから考えて行動する子供には批判的な思考があると聞きます。「本当にそうかな」と疑ってみるような。

古川：批判的思考といえば、川村さんはデザインをする時、しらみつぶしに可能性を考えるそうじゃないですか。実は僕らが使っている「Salon De ∫u Ken」のロゴデザインも川村さんの作品で、できあがるまでの過程では、いかに客観的・俯瞰的に可能性を捉えられるか、かなり試行錯誤されましたよね。そういうアプローチが、もしかしたら数学的と言えるかもしれない。

＜川村さんの作った「Salon De ∫u Ken」のロゴ＞

実は建築の世界でも答えは無限にあります。それをできるだけ俯瞰して、一番正しいものは何か考える。そういう作業は必ずやっています。宇宙まで行き、そこから地球を見ているくらいの感じで。

数学で身につくのは「鳥の目線」だ

澤：物理学者のフリーマン・ダイソンは「科学者には“鳥の目線”と“カエルの目線”の人がいる」と言っています。鳥の目線の人は、俯瞰的にものを見る。カエルの目線の人は、小さいところをじっくり分析していく力を持つ。それで言うならば、数学をやっている人は鳥の目線、物理をやっている人はカエルの目線ですよね、っていうんです。

「俯瞰的に見る」「批判的に思考する」は、数学をやっていると身につく大事な2つの要素です。そういう意味では、ちょっと苦手になったからといってドロップアウトするのはもったいない。そういう教育にならないようにしたほうがいいですよね。

川村：数学の人にはカエルの目線はないんですか？　建築もデザインも、最終的なアウトプットを作らないといけないから、どちらの目線もバランスよく持っていないと駄目なんですよ。デッサンなんかもそうで、ディティールばかり書いていると形が狂ってしまう。だから立ち上がって距離を置いて見て、また近づいて描いて……を繰り返します。

澤：もちろん数学でも全部が全部鳥の目線ではなく、カエルの目線もあります。だけど、問題が解ける時は、あまり分析的ではないんですよ。一瞬にしてバッと全部が見えます。

数学ではどちらかというと、概念を作り上げていることのほうが多いですね。たとえば、多くのものが整理できる「AならばB」という概念はないかとか。数学では「抽象化して束ねる」という作業がすごく多いです。これは計算をするのとはちょっと違うので、「数学科の人は算数が苦手だ」という話があるんですけど（笑）。

それと関連する数学の特徴に「単純化」があります。3つのりんごと3つのみかんは違うものじゃないですか。だけど、数学をやっている人にとっては「3」という数字に意味があるだけ。建築家やデザイナーは、最後は「もの」を表現しなければいけないから、りんごならりんご、みかんならみかんが必ずついて回ると思うんです。数学ではそれを削ぎ落としていって、概念として整理しようとします。だから、カエルの目線もゼロではないけれど、鳥の目線が強いんでしょうね。

抽象化をめぐっては、ほかにも面白い話があります。「点の面積」を考えてみましょう。点は面積が0ということになっていますが、実際にマジックで点を描いたら、絶対に面積があります。線についても同じです。

古川：「面積0の点」は概念でしかないですからね。

澤：そう。人間は抽象化ができるけれど、自分がそうしていること自体には意外と気づいていないんです。点や線の面積と似た話では、三角形の合同条件があります。現実にはまったく同じ図形を描くことなんてできません。でも、頭の中には合同の図形がある。どんどん抽象化する方向にいくのが数学です。

人間は抽象化を成長過程で身につけていきます。認知心理学や教育で有名なピアジェという人がいますよね。下の図は彼の『思考の誕生』という本に出てくる事例です。

大人になると、6番目は黒と白の碁石の数が違う、7番目は同じだとわかります。でも、小さい子供たちには6番目と7番目が一緒に見えてしまうんですね。つまり、最初は量的な概念に支配されているけれども、次第に数という概念を学んでいく。7番目・8番目の碁石の数が白黒どちらも同じだというのは、抽象化するからこそ、わかるわけです。

次元とは「Excelの表」だ

澤：次は、みんなで「次元」について考えてみましょうか。1次元はわかりますよね。2次元も、3次元もわかりますよね。でも、4次元ぐらいになると、どうですか？

川村：1次元は線、2次元は平面。3次元は立体。4次元になると時間が入ってきて、急に図形ではなくなっちゃう。

澤：では、5次元になると？

川村：う〜ん……。

澤：僕は大学の時、6次元ぐらいまで見えるようになってしまって、このまま大学に残っていると神様の領域に足を踏み入れそうだと思い、進学をやめました。

古川：澤さん、僕ら3次元までは直感的にわかるんだけど、4次元ぐらいから戸惑うんだよ。

澤：「4次元」というと「時間が入ってくる」という人が多いじゃないですか。「次元」というと“ものの形”だと思うんですね。で、３次元までは現実に知っている。４次元っていうと、まあ、一般的には「時間」って教わることが多いのかな。相対性理論やらタイムマシン、みたいな議論で「４次元」っていう話になるからだと思います。ものの形を探る学問を「幾何学」と言いますが、まさに幾何的にはそういう説明がわかりやすいから、そう言うんです。でも、そんなことではないんですね。次元のイメージを理解するのに一番わかりやすいのは、Excelの表です。たとえば、先生がクラスの成績をExcelで管理していたとしますね。そこに生徒の名前だけが並んでいる場合、1次元です。横に国語の成績があったら2次元です。さらに算数の成績があったら3次元、理科の成績があったら4次元。幾何的に考えると頭がごちゃごちゃになるけれど、単なるExcelの表だと思えば、4次元も5次元もそれほど難しくないんですよ、実は。

古川：4次元とはつまり、変数が4つ並んでいるということ？

澤：そういうことです。

現実にないものは、なかなか理解できない

澤：幾何的な次元をめぐっては、こんな話があります。僕が大学1年生の時に教わっていた鳥居修晃さんという有名な認知心理学者は、先天盲開眼者の視覚世界を研究していました。先天盲、つまり目が見えない状態で生まれた人ですが、中には、手術すると目が見えるようになる人がいるのだそうです。そういう人たちの視覚はどうなっているか。われわれが美術館に行って風景画を見ると、奥行きが感じられますよね。もともと絵は平板で2次元だけれど、それが3次元に見えるわけです。けれど、手術によって目が見えるようになった先天盲の人は、絵に奥行きが感じられないのだそうです。成長する過程でそう感じるような構造が作られていないから。

古川： 2次元から空間を読み取るトレーニングができていない？

澤：そういうことではないかと思います。先ほど「自分は数学科に行って6次元が見えるようになった」と言ったじゃないですか。私たちは奥行きのある世界に生きているから、3次元という概念は次第にわかってくると思うんです。それと同じように「3次元しかわからない」と思っていても4次元がわかるようになったり、次は5次元がわかるようになったりすることが、けっこうあるのかもしれません。数学をやっていると、次元についても広がりが見えてきます。

もう一つ、人間は意外と頭が固いって話をしますね。たとえば、-1、-2のような「マイナスの数」がありますよね。あれを発見したのはインドの人で、西暦700年ごろにはもうわかっていたそうです。でも、ヨーロッパの人たちがマイナスの数字があると納得したのは1700年ごろ。インドの人がマイナスを発見してから1000年ぐらい後に世界に広がったわけです。

現代に生きるわれわれは「マイナス」を理解していて、「X+2=1の答えは-1だ」とわかります。でも、この概念を多くの人が納得するようになったのは、けっこう最近の話なんです。

川村：理論上はマイナスが存在するけど、目の前にはマイナスが存在しないから、理解しづらいと。

澤：そう。人間はそれほど頭が柔らかくなくて、現実にないものは、すぐには理解できません。算数は、石で数を数えるところから始まりました。石が「-1」になることはないじゃないですか。

古川：そんなことになったら、びっくりするよ。

澤：だけど、川村さんも古川さんも、-1や-2の概念がわかっていますよね。みなさんがわかっていてできることも、昔の人は意外と理解していなかった。数学の能力は抽象化です。でも、現実に引きずられてしまうのが人間のサガです。現実に引きずられがちな人間と抽象化をする神様のせめぎ合いが数学なのかもしれません。

ものごとの解決策には「引き算」もある

川村：ぜんぜん関係ない話をしてもいいですか？　いま、足し算引き算の話を聞いて思い出しました。デザインをやっていると、特定の文字や商品を目立たせたいという要望がお客さんから出てくるんですよ。でも、普通の人は足し算で解決方法を考えることが多い。だから「文字を目立たせてください」と言われるのではなく、「大きくしてください」「太くしてください」と指示されてしまうんです。でも解決方法には、実は引き算もあります。たくさんある要素の優先順位を決め、引いていくことで、目立たせたいものがより目立つようになる。だけど、たいていの人は足す方向にいくから、結果としてどれも目立たなくなりがちです。これはデザインあるあるですね。

澤：数学的な考え方では、補助線を足すような「足す」方向ももちろんあります。だけど、数学で「この数式が美しい」「エレガントだ」と言われるのは、シンプルなものですね。物事をシンプルにしていこうという発想は、デザインと数学で意外と近いのかなと。

川村：建築にもそういう傾向はありますか？

古川：建築は、シンプルにしていかないと成立しません。最初はフリーハンドでごちゃごちゃ描いて考えます。そうしてたくさん描いた線をそぎ落とし、「8畳間」「6畳間」のような抽象的なものにしていく。そうしてシンプルな骨組みを考えていく作業だと思うんです。数学の発想には建築っぽいところがありますね。

澤：僕が郵政省で仕事をしていた頃は「A4の紙1枚にまとめるのが上手ですね」とよく言われました。たくさんの紙を使って説明すると、大変なことになるじゃないですか。でも、僕はなるべく少ない量で本質的な部分だけ伝えようと思っていました。単に面倒くさがり屋と言えばそれまでだけど、そういう思考は数学で身についた気がします。

古川：ちょっと質問。澤さんは考える時に、たぶん文章ではなく、図表で考えるでしょう。キーワードをワーッとA4の紙に書いたりしながら。そんなことはないですか？

澤：そうですね。A4の紙に鉛筆で書いていきます。すると、「これとこれは近い」「これとこれは遠い」「どうもこのあたりが抜け落ちている」と見えてくる。そういう感じでものを考えることが多い気がします。知識量を増やすというよりは、本質はどこにあるのかを見定める。それが数学をやっている人の特徴かもしれません。

数学をやる人はDNAに逆らっている

澤：抽象化ついでに、ちょっと寄り道しましょう。小学校の初め頃、3×2と2×3は一緒だという「交換法則」を習いましたよね。なぜそんな当たり前のことを教わるのか、みなさん疑問に思いませんでしたか？　でも、そうならない例が高校になると出てくるんですね。最近は学ばなくなったらしいのですが、一次変換とか行列、と言われているものがそれです。この話をしても難しいので、もっと単純な例をお話してみましょう。たとえば、調味料を入れる順番の「さしすせそ」――砂糖・塩・醤油・酢・味噌。あれを「そしすせさ」の順にすると味が変わってしまうから、交換できません。交換法則が成り立たない例はほかにもたくさんあります。小学生の時にそう言ってくれていれば、ずっと高校の数学が学べることを待ち望んだか、先に勉強しようと思ったはずなんですよね。この経験が学校教育を考えるきっかけになりました。

抽象化するからこそ、交換できないものがあるから、交換できることはその特別なことっていうことになるんですね。でも、それが特別なことは、小学校の時はわからない（笑）

今度は、ちょっと体を使った実験をしてみましょうか。

僕はピアノを弾くので、その例でお話ししますね。両手を開いてください。両手の指を同時に、親指、人差し指、中指……という順に指を動かしてみてください。簡単でしょ。でも、たとえば右手は、親指、人差し指、薬指、中指、小指という順で、左手は小指から親指に同時に動かすのは難しいんです。みなさん、どうですか？

川村：辛いですね。

澤：これはけっこう辛いんですよ。なぜか。DNAでは、親指、人差し指、中指の順に両手を動かすよう成長がプログラムされているんです。一方を、小指、薬指、中指、人差し指、親指の順にすると、とても辛いのは、DNAに逆らうから。でも、ピアノの練習をしている人たちは、DNAのとおりにならないよう、成長をぶった切っているようです。だから弾ける。つまり、ピアノができる人たちは成長しているのではなく、成長していないことになります。

数学もこれと似ていて、抽象化した世界で頭が痛くなりそうなことを一生懸命考え続けるんですよね。たとえば「-1の石ころって何だっけ」とか「普通は特定の数を二乗すると正の数になるけれど、負の数になることもあるのでは」とか。これは実際に見えているものから考えられる基本的な概念に逆らう作業だから、非常に大変です。それを続けるのは、お寺で修行するようなもので、だからこそだんだん”神様の領域”に近づいて行くっていうお話になるんですよね。

数学科に行くと、みなさん黒板の前でにこやかに数式を書いています。すごくいい人たちなんですよ。なぜか。「現実」にあまり縛られないんです。現実がどうかよりも、論理的に正しいかに興味がある。ある意味では悟りを開いているんです。

みんながみんなそうなると困るかもしれない。でも、僕はそういう世界に入れるところに数学をやる意味があると思っています。これが「数学の気持ち」という今日のお題への答えになっているかはわかりませんが、楽しそうな世界だと感じてもらえたらと。

数学の新たなネーミング「あまの学」

川村：話を聞きながら、「数学」の新しいネーミングを思いつきました。特徴を表すキーワードをいろいろ考えていて、1つ出てきたのが「ひねくれている」。数学をやっている人は物事を斜めから捉えているのかなと思いました。それから、数学に苦手意識のある人はやっぱり多いじゃないですか。だからネガティブな印象を持たれたり、ちょっと嫌われたりする。そうした印象から思いついたネーミングが「あまの学」。

澤：「あまの学」。あまのじゃくだからということですか？

川村：そうです。あまのじゃくは、ネガティブなだけでなく愛すべき存在でもあるじゃないですか。ただの嫌われ者ではなく、ちょっと愛されキャラ。そこが数学とちょっと似ているかなと。今日出てきた「神様」というワードとの関連で言っても、あまのじゃくは神様に近づこうとして踏んづけられ、下から見上げていますしね。

澤：なるほど、確かにそうですね。僕は数学をやっている人が1つの組織にたくさんいる必要はないと思います。でも、1人ぐらいはいてもいい。郵政省に勤めていた頃、会議で話がまとまらないと、僕のほうを見る人たちがけっこういました。「こうじゃないですかね」と自分の考えを話すと、「じゃあそれでいくか」となる。議論が白熱する時はあまり頼りにされないけれど、どうも話が整理できない時に1人いるとうれしい。数学をやっている人がそういう感じでいてくれたらいいかもしれません。そういえば、最初の頃に女帝エカテリーナの逸話、話しましたね。

川村：普通の人とは違う視点を持っていますからね。

澤：そう。ひな壇にのる必要はないけど、こっそりいてもいいかなと。

川村：そこも足元から見上げているあまのじゃくに似ていますね（笑）。

最後は感覚

古川：澤さんは議論が行き詰まった時、少し違う視点から俯瞰で見て、「この言葉でまとめられるんじゃないの」と言い当ててくれる。その澤さんという存在は、数学によって支えられている――。でも、数学的な人はそれほど表に出てこないですよね。何だろう。教育の問題かなあ。

澤：それもあるかもしれません。だけどやっぱり、日本では「エビデンス（証拠）に基づいて政策を決めましょう」というEBPM（Evidence-Baced Policy Making）的な発想が薄かったのかもしれないですよね。どちらかというと法律で縛る方向にいき、数や量でものごとを測る方向ではやってこなかった。

古川：澤さんが否定的に捉えている感覚的な世界というか、体育会系的な世界というか。

澤：そう。それが全部駄目とは言わないし、世の中わかっていないことが多いし、データはあくまで全部は説明できないから、最後は感覚を大事にすべきだと私も思うんですよ。ただ、無数の候補の中から何か1つを選ぶことはデータではできません。物事を絞る時には数字が使えますが。

僕はずっと行政の世界にいて、データに基づいて物事を判断する部分が弱いと感じてきました。しっかりデータでターゲットを絞っておけば、そこからちゃんとした正解に到達する角度は高くなる。だからみなさんには、これからぜひ数学を学んでもらえたらと思っています。「数学をやった人の気持ち」なのか、「数学の気持ち」なのかわからない話になってしまいましたが……。

古川：終わりの時間が来ました。どうしましょう。質問のある方はいますか？

A：いいですか？　いま数学的つまり論理的なことと、感覚的なことを分けて話を進めていましたよね。でも、論理をとことん突き詰めた先に直観があるとは考えられないでしょうか。直観で選んだものとしばらく考えて選んだものが一緒だという研究があるそうで、そう思いました。

澤：僕がした話では、鳥の目線とカエルの目線の話に近いと思います。数学で証明問題が解ける時は、詰めて考えるわけではありません。直観なんですよね。いろいろな情報をインプットした後、「どうもこれが正しそうだ」とわかる。逆に言うと「ああ、もうこれは絶対にこうだ」とわかるから、あまり考えなくても証明が書けます。この現象は、たくさんの数学者がエッセイなどに書き記しています。多くのインプットが整理され、答えが見えてくる。数学の世界ではそういうことだと思います。

A：具体的にはどうすれば、そうなるのでしょうか。

澤：やっぱり、煩悩のない境地にいかないとわからないかもしれないですね（笑）。

A：なるほど（笑）。

古川：僕のいる建築の世界では、いろいろな情報をインプットし、手を動かしていくんですよ。すると朝起きた時、何かができあがっていることがあります。何でしょうね、これは。

澤： 先ほどのA4の紙に書き出しながら考えるという話に戻ると、できていない時は見ていて何か足りていない感じを受けるんですよね。どうも味付けがいまひとつで薄味だという感覚がある。そのあたりを探っていくと、突然「あ、けっこうおいしい味付けになりそうだ」とわかる瞬間が訪れます。似たものを集め、何か1つに決める仕事をしている人全体に共通する話ではないかと思います。これは数学に限らず、古川さんが設計される時も、川村さんがデザインされる時もそうではないかと。

古川：澤さん、その話はすごくよくわかる。できていない感、何か足りない感があるんですよ。川村さんもそうですよね？

川村：僕が作った「Salon De ∫u Ken」のマークも、最初のアイデアからだいぶ変わったじゃないですか。その過程では「まだ完成していない」と思いながら走っていくわけですよ。そうして考えたり、ブレストしたりしているうちに、新しいアイデアを思いつきます。

澤：どうすればもう少しシステマティックに、この何か足りない状態からパッと答えにたどりつける、ということを説明できないものかと思っていたら、デザイナーの吉岡徳仁さんの『みえないかたち』という本に、それらしいことが書いてあったんです。それで読み進めていったら最終章に「でも最後の最後に雲の中から一筋の光が見えるような瞬間が訪れるのはなぜか説明できない」という趣旨のことが……結局答えは書かれていませんでした（笑）。でも、吉岡さんの書いていることはそのとおりだと思います。証明問題の解き方に気づく時、仕事の解決策が見つかる時は結局、人間の特殊能力でやっている。それがいまのところの結論です。

古川：僕にも建築の神様が降りてくる時がありますよ。

川村：デザインの場合、パッと思いついたアイデアは、実はありきたりなことが往々にしてあります。頭の中に残っている何かが出てきている。そういうアイデアはあまり信用しないようにしないと、斬新な案は出せません。やっぱり考えつくした先、100案出した先でないと見つからないとは言われていますね。

A：ありがとうございます。

ものの考え方を身につける意味でも数学を学ぶ機会を

古川：Mさんという方からチャットで質問です。「数学をやることは、神様に近づくことですか？」。

澤：Mさんは私の数学科の後輩です。チャットの続きを読みますね。「トポロジーの世界に入ろうとして、2次元までは見えたけれど、3次元が見えなくて数学に挫折した」。Mさんは数学をやっているので、難しい言葉を使われているけれど、面白いですね。先ほど言った幾何的なものの見方と「群論」という数学の道具立ての話が書いてあります。道具を使うことで次元が見えることはあるので、すごくよくわかります。ただこの話は、数学をやっている人以外にはわからないかもしれません。

古川：なるほど。Oさんからもコメントをいただいています。4K会議の話。

澤：ああ、4Kって「根性・経験・勘・コツ」のことですね。エビデンスの重要性っていうお話をしましたが、数字を理解できる人がもう少し前面に出てきてほしいです。去年・一昨年と大学の先生に講演をさせていただく機会を頂いたのですけど、その時も、「世の中には数学ができる人々の力が必要だ」ということをお伝えさせていただきました。そうでないと、なかなか変わっていきませんから。

今日もエビデンスを使ったデータサイエンスの話をしていたのですが、そのプロジェクトでは、そもそものデータの取り方が間違っていたんですね。僕にはそれがすぐわかりました。でも、すでに誤ったデータを使って仕事を始めてしまっていると。それで「どうしたらいいでしょうか」という話になった。正しいデータではないのですから、どうやっても正しい答えは出てきません。やっぱりデータの品質がわかる人たちが、もう少し社会に入って、そういう無駄な仕事とか、仕事の手戻りを防ぐということ、もっと恐ろしいのは、間違いに気づかずにプロジェクトが進むということで、それを防ぐ仕組みを作りたいですね。

古川：Sさんからも、似たコメントがきています。

澤：Sさんは中学校で数学の教員をされています。プログラミング教育が大事なのか、っていう話ですね。いまは何となくプログラミング教育の方向にいっています。もちろんそれはそれで進めればいいと思うけれど、数学はもう少し基本的なものの考え方にかかわる科目なので、そちらの教育にも力を入れたほうがいいと私も思っています。僕自身もこの話はいろいろなところで発信していきたいと思っています。

古川：Mさんからまたコメントがきていますね。EBPMについて。

澤：ははは。Eは「Evidence」ではなくて「Emotion」って解釈ね（笑）。

古川：でもいいですね。「Emotion」は「根性」と訳されているけど、「情念」「情熱」のようなニュアンスでしょうか。

澤：通常は「EBPM（Evidence-baced Policy Making）」ですけど、日本は「PBEM（Policy-based Evidence Making）」だとよく揶揄されますよね。要はポリシーが先に決まっていて、それに合うように統計処理してくれと言われることがものすごく多い。「数字作ってくれ」みたいな話。それはやっぱりよくないと思います。Policy-basedでもいいと思うけれど、EvidenceをMakingしてはいけない。やっぱりPolicyを作ると同時に、Evidenceが適切な範囲に入っているかどうかチェックするくらいの感じがいいのかなと。

数学からデータサイエンスの話が派生しました。今日最初に「数学（mathematics）とはものを考えることだ」という話をしたとおり、現在は社会全体が数字を使おうという議論になってきています。いま教育に関わっていて、ものの考え方を身につけてもらう意味でも、数学が学べる機会を増やした方が良いと考えています。今日の話でそのあたりが伝わったらうれしいです。

古川：では、今回の「さろんですけん」はこれにて終了します。またいろんな話題を提供していければと思っています。今日はこのへんで。

３人が、そして、時にはゲストをお呼びしてのゆるゆるトークですが、時々面白い発見があると思います。

それを３人も楽しみに続けています。ぜひ、気軽にご参加ください。

コアメンバープロフィール

川村貞知（かわむら・さだとも）

アートディレクター／グラフィックデザイナー。’70年東京生まれ、藤沢育ち。

東京藝術大学デザイン科卒業、同大学院修了。

電通アートディレクター、文化庁派遣芸術家在外研修員(NY)を経て、’03年Sadatomo Kawamura Design設立。

プランディング、デザインコンサルティング、CI、VI、ロゴ、パッケージ、キャラクターなどを手掛ける。

澤尚幸（さわ・なおゆき）

一般社団法人Community Future Design代表理事。三重県生まれ。

1991年3月東京大学理学部数学科卒業。同年郵政省に入省。省庁再編、郵政公社化、民営化に関わる。

退社後の2015年12月、当社を設立。現在は地方自治体や企業等の地域活性化やその政策立案へのアドバイスや支援などを実施。行政・地域のスマート化・データサイエンスの活用、GIGAスクール時代だからこそのリアルな学び、デザインによる地域活性化などに取り組んでいる。

古川泰司（ふるかわ・やすし）

アトリエフルカワ一級建築士事務所代表。一級建築士。住宅医。森林インストラクター。おもちゃコンサルタント。

武蔵野美術大学建築学科卒業後、’88年筑波大学院芸術学系デザイン専攻建築コース修了。

建築事務所や工務店に勤務後、現在の事務所を設立。林業、製材、職人をつないだ、地域の木を生かした建物の設計を実施。最近では、住宅医の資格を活かしながら、空き家活用で地域の空間資源再生を通した地域再生やコミュニティづくりにも取り組む。

関連記事

【対談】地域と「よそ者」がつながるには（後編） デザインとは何か？【オンラインイベント第1回動画の要約】 オンラインイベント第7-B回開催のお知らせ 【対談】「農業女子」という働き方（後編）