2024年5月23日更新　投稿者 CFD

BARこふで #0　 統計をぬる燗で

～平均にもほどがある～

※本記事は５月２日に配信された「BARこふで#０『統計をぬる燗で～平均にもほどがある～』」から、その一部をテキスト化、編集を加えたものです。

＃０ スピーカー紹介

プロローグ

澤：こんばんは。GW、みなさん、いかがお過ごしでしょうか？

GWに入る少し前、新幹線で広島から東京に戻ってきたのですが、車両の9割くらいが外国人でした。欧米人が非常に多いですね。円安で、外国人にとっては、日本は非常に物価が安く感じられるそうです。

一方で、日本人は海外旅行に行くとあまりに滞在コストがかかるので、日本で過ごす人が多いとのこと。

いずれにしても、国内観光地は人口密度が高いことが容易に予想される。ということで、全国を回る仕事の私も、GWは東京で巣ごもりです。

さて、このBARこふでは今日0回目、プレ開催という感じです。

今までもZOOMでイベントみたいなものをやったりしましたが、これまでのものは、どちらかというと双方向で「誰かが喋ったことに対して意見を述べてもらいディスカッションしましょう」みたいなものが多かったので、喋る人も結構考えなきゃいけなくて大変だ、ということもあり、なかなか長続きしないということがありました。

それでふと思い出したのですが、昔、東京FMでサントリーが提供していた「サタデー ウェイティング バー」という、誰かが色々喋ってるやつを聞き耳立てて聞いてみるっていう、面白いラジオ番組があったなと。結構前にもうなくなっちゃってるみたいなんですが、それを思い出しまして。

私は全国でいろんなところに行って、いろんなお友達と話す機会がありますが、 ただただ話すことを聞きたい時に聞いてもらって、その中から何かお持ち帰りいただけることでもあったらいいかな、というぐらいの感じで、緩くやってみたいなと思っているところです。どこに向かうか全く予想がつかないのですが。

うまくいけば続きますし、面白くなかったらやめちゃってもいいし。あと、僕が地方に行く機会を使って「ちょっとこれから1時間だけお話してみませんか」とどなたかをお誘いして皆さんに特別公開、みたいなことをやってもいいのかなと。そういうフラット配信型で色々やってみよう、と思っています。

私自身は結構コミュ障で、話すことがそんなに得意ではないのですが、友達の中にはお話上手な人がたくさんいてくれて、 その人たちとお話していると、その会話自体からの学びも勿論大きいのですが、何よりも、会話を返す中で自分のやってることが色々見えてくるという体験が多くて。そんな体験が人とお話をする大事な要素なのではないか、などと考えながら話を進めてみようかなと思っています。

さて、今日の友人、そろそろ来るはずなんだけどな・・・。

今晩のツレ～縁の深い後輩～登場

澤：来ましたね、こんばんは。

槙田：こんばんは。広島からです。

澤：広島ですか！

槙田：尾道です。

澤：え？そうなんですか？なんで？

槙田：映画監督の大林宣彦好きなもので。高校時代、青春18切符で鈍行を乗り継いでロケ地の尾道に行ったことがあり、以来、尾道は心の故郷です。

澤：槙田くんが映画好きだなんて知らなかったなぁ。槙田くんとは、大学も一緒、数学科という学科も一緒、サークルも一緒で、なんやかや、職場も結果として一緒になったという仲で、ある意味「ずっと一緒」でありながら、先輩後輩で時期がずれていることもあり、実はそんなにちゃんと深く話したことはない、という間柄なのですよね。

ですので、今日は、過去のお話を色々と聞いてみながら、この先どうします？っていうお話も聞きたいなと。とにかく、槙田くんについて全般的に色々聞いてみよう、そんな企画です。

なぜ数学

澤：これは何度も聞かれたことがあると思いますけれど、どうして数学をやろうと思ったんですか？

槙田：いつもは「ドラえもんの四次元ポケットが見たかったから」って答えていますが、澤さんにはホントのことを言いますと(笑)、物理学も面白そうだと思っていました。ですが、あの学科はちょっと私のテストの点では手が届かなかった（苦笑）。

小さい頃はそろばん塾に通っていて、それが数と触れる初めての世界でした。中学に入ったらxy平面とy=ax+bが出てきて、図形と数式が絡み合っていくという体験が衝撃的で、それで数学が面白くなってきたんですね。

高校になると、当時の私たちの時代では行列計算が出てきます。ここで随分スランプになってしまいました。そんな時に「大学への数学」という高校生向け月刊誌に出会いました。その「大数」には高校教科書にはない線形代数の世界「固有値・固有ベクトル」が書いてあって、これらを理解できるようになったら、スランプを脱して世界が突如パーーっと広がったんですよ。

澤：固有値は、どちらかというとパーッと広がるのではなくて、そこに縮約してくるというか、縮退してくるという感じの話のような気がするんですけれど・・。

槙田：確かに、固有ベクトルという基底のおかげで世界がすっかり整理されてしまいました。そんな風に数学の扉がパーーっと開いてくれる。その感覚が面白かったんですね。

数学って美しい

槙田：数学って、言い換えると、美しいものなのです。それが原体験になって、世の中を見える化・可視化するということが私の関心になっていきます。これが統計への関心にもつながっているかもしれません。

澤：なるほどね、面白いね。やっぱりみなさん「美しい」って言いますよね。

槙田：数学の美しさ。世の中のどれだけの人とこの感覚を共有できるかわかりませんけれども、澤さんとは共有できる。この「美しい」って、英語では何て言うんでしょう。ビューティフル、エレガント…

澤：解法をエレガントって言うかもしれないけれど、数式をエレガントとは言わないですよね、多分。

行列をやったときに、空間がくしゃくしゃってなるじゃないですか。くしゃくしゃってなる感じが、「なんでこんなものでちゃんと表せるんだろうな」って思ったのが私は結構楽しかったのですが、行列計算って、私たちの時代とは違って、今の高校数学では習わないらしいですよね。

槙田：そうみたいですよね。

澤：小学校の時に「１×２」は「２×１」と同じということを習うじゃないですか。数学の言葉を使えば交換法則とか結合法則とかになりますが「はいはい、当たり前だよね」って思いますよね。

でも、高校でそれが当たり前ではない世界が実は存在する、ということに気付かされたのが、私にとっては数学を結構楽しいなと思った最初だったんですね。

だから、その楽しい感じを今の高校の人たちは学ばないのか、と思うと残念な気がします。

槙田：小学校のテストの答案で「1×2」は○なのに「2×1」はバツ（✕）をつける先生がいるという話を目にして、本当にそんなことがあるのだろうか、と思ったことがあります。

澤：都市伝説ではなくて、本当にあるみたいですね。

槙田：そんなことされたら、数学以前に算数のことを嫌いになっちゃいますよね。

澤：フィールズ賞（数学界でのノーベル賞とされる最高位の栄誉）を日本人で受賞された森重文さんっていらっしゃいますよね。その方がお話されていたのですが「どちらで掛けても答えが一緒だということが数学的にはすごい意味がある、ということを教えなくてはいけないのに、どちらが先でないとダメだと言っているのはダメだ」と強く仰っていたのがすごく印象に残っています。

槙田：わかりみ、深過ぎます。

澤：それが先ほどの「行列は交換できないけれど、実数や整数は交換できますよね」ということとある意味イコールですよね。

交換できるものと交換できないものがある

澤：数学をやっている人は当然そう考えられると思います。そしてそれはまた、順番があるかないか、という話でもあると思います。

私がよく使う例えなのですが、調味料の入れ方「さしすせそ」って言うじゃないですか。あれは、調味料を入れる順番を変えると多分違う味になりますよね。だから調味料には交換法則が成り立たないって、よく説明するのですけれど。

槙田：美しい。

澤：学校で児童に教えるという先生の立場を考えたときに、言われたとおりにやるという話と、でも現実は交換できるという話と、両方ともを教えてもいいような気がします。

槙田：なるほど、順序をいい加減に扱えば台無しという世界もある。そういうことなら話についていけるかもしれない。

澤：ルールだからやれ、と言われていることと、どちらの方法でやってもやっぱり結果は同じだっていう、その両方があるよね、ということをきちんと教えるんだったら、先ほどの✕を付けてもいいような気がするんですよね。

今日はこういう順番を守って式を作ろう、という指示を出したから、それができるようにする学びです。だから順番が守れていなかったら✕ですよ、って説明されたら、私はその先生は結構いい先生なんじゃないかなと思ったりします。

ホントは苦手でした

澤:　ここから、槙田くんはどうして統計をお仕事にしようと思ったんですか？という今日のメインの話に繋げていきましょうか。

槙田：澤さんに白状すると、大学の教養科目で取っていた統計学や経済学も苦手だったんですけれど。

澤：私は今でも統計は苦手ですよ。

槙田：数学科の学生はたいてい大学院に進むという感覚がありましたから、私も人並みに大学院の入学試験、院試を申し込んでいました。けれども一方で、就職しようとしている同学年の人たちもいましたので、社会のことも少しは見ておかなくちゃ、と思って、会社説明会を聞きに行ったんです。そうしたらあるリクルーターが「この中で院試を受ける人」って聞くから「はい」って手をあげたら「そうか、君にいい話があるよ。大学院試の安い模擬試験があるよ。公務員試験っていうんだけどね」って(笑)。

ちなみに、澤さんは以前オンラインイベントで「6次元ぐらいまで見えるようになってしまった」と言ってましたが、私が見えてるつもりだったのは2次元に留まり、3次元さえうまくいけず挫折しました。

ま、そんなこんなで公務員試験を受けて、そのあとは話が長くなるので割愛しますが、結果、今のところに勤めています。

澤：じゃあ、統計をとりわけ望んでやろうとしていたわけでもなかったということ？

槙田：数学はそれでもやっぱり好きだったので、それを活かせる仕事がしたい、とは考えていて。

澤さんが以前勤められていたところの保険数理，その方面への選択もあったのですが、もしもそこへ勤めるようになると全国にある支店のどこかへの転勤を免れないだろうと。この点、私が選択した勤め先は東京の拠点だけなので引っ越しをさせられることはないだろうという思惑もあって。。

澤：けど、海外に行かされていた時期もありましたよね？

槙田：はい。実際には転勤を２回してしまっています(笑)。

澤：なるほど。私は地方に行きたくてしょうがなくて選んだ仕事だったのに、気付いたら１年を除いてずっと東京にいたというオチでしたね。その分今は思う存分地方に行きまくっていて、反動ですね。

なるほど随分違いますね。けれども、その後、お互いの勤め先が合併して一緒になっちゃいましたね。

統計にまつわるモヤモヤ感

澤：去年久しぶりに槙田くんにお会いした時にもこの話をしたのですが、統計っていまだに私はよくわからないんですよね。

方法論として、数学を使っているという意味では物理と一緒じゃないですか。どうも答えが決まらないというか、答えの中に解釈が入るというか・・。ここが私はいまだにすっきりしない。物理も今ひとつ苦手意識があります。

一昨年度に遅ればせながら修士を取った時に統計を使ったので、そのすっきりしない気持ちをいろんな人に相談したら、「そういう気持ちになるしかないです」って怒られて。

いやそう言われても、答えは1つでしょう、という・・。「できるできない」「イエス・ノー」でやってきた頭の感じだと、「これを解釈してください」みたいな話になるのが物凄く怖い。

逆に言うと、「本当に『これはこういう答え』って言っちゃって大丈夫なんでしたっけ？」ということも気になるし。その辺のモヤモヤを感じながらずっと仕事していたというか。

確率はそうでもないけれど、統計を使う時は、なんかそのモヤモヤ感がいまだに全然こう、スコーンって落ちないな、と思うんですけれど、そんなことないですか？

槙田：澤さんがここで言われてる統計って、平均・分散・標準偏差といったものではないですよね。それよりも、もっと大きな統計だと思います。すなわち、社会を数で計って理解するための統計ですね。

社会を理解するために統計は使われる。けれども一方で、統計があるからといってそれで世界がわかったつもりになっていいのかというと、そこは丁寧に考えてほしいというのが私の考えです。

このことについては実はいくつか「引き出し」を用意しましたので、お話しさせてください。

統計の残酷さと公平さと

槙田：Covid-19が急拡大しだした4年前、ニュースはコロナ感染者数を1日刻みの棒グラフで連日報じていました。

その感染者数の報告には奇妙なクセがあって、コロナ検査が週末お休みになる関係で週明けの数は周期的に落ち込むことがありました。そんなアノマリーの影響を取り除くために、”慣らし計算”処理がされてもいましたが、マスコミも「移動平均」という統計用語を使ってこれを報道していたことがありました。

そんな当時の新聞コラムで、こんな一節がありました。（2020年4月27日 日本経済新聞 朝刊 春秋）

これは、米国の経済学者トーマス・シェリングの言葉を紹介していたものなのですが、

統計って、このようにすごく残酷で、対象を無機質な「ただの数」にしてしまうんですね。

けれども、だからといって統計はけしからん、嫌いだ、という話になるかというと、別の考えもあると私は思っていて。

統計は、実はすごく平等なのです。金持ちであれ、貧乏人であれ、どちらも１人、と平等にカウントされます。選挙でも、みんな１票ですよね。

そんなふうに、数にはどのような文脈があるか、考えてみましょうと。

数についてストーリー・テリングを行うことで、数の文脈、コンテクストをユーザーに理解してもらって、そうして使われてこその統計だと思うのです。

社会現象をいろいろな切り口で統計に落とし込んで、いくつもの数字で測って分析して、けれども、下すことのできる決断は結局のところ、１つしかできません。

その1つだけの決断が、本当にそれでよかったのかどうか、これも統計のいろいろな切り口で考えてみることになると思います。

これでお答えになっているでしょうか。

澤：そうそう。統計で話をするときって「何が分かっていないのか」を言ってほしいなという気がしています。

どういう人にアンケートをとるか、どんなアンケート文言にするかによっても、結果にバイアスがかかることがありますよね。「どういうバイアスがあり得るのか」を言ってほしい。

槙田：それに、統計には必ず誤差が伴います。母集団の一部をサンプリングして数を作れば一定の標本誤差は生じます。アメリカのCNNテレビが世論調査を紹介する時には、画面の隅にプラスマイナス（±）のエラーが必ずといっていいほど表示されています。

対して、日本の世論調査や統計の報道ではあまり目にすることはありませんが、それでも、例えば総務省統計局や内閣府世論調査のウェブサイトには標本抽出の仕方や標本誤差の情報、調査票様式も掲載されています。

澤：そういう背景情報を明示してほしいですね。

「こういう数字を出したいという意図があるからこういうアンケートを取っているな」と思ってしまう統計も見受けられるじゃないですか。

例えば「体育館は要りますか？」という問いと、「体育館を作るのはよいけれど、税金が上がります」っていう問いが仮にあったとします。そうしたら、後者の場合は、税金上げてまで体育館は要らない、って答える人はたくさんいるような気がします。

それを言わずに「体育館は要りますか？」だけアンケートを取って、「みんな体育館が欲しいと言っています」という結果を出しちゃう、というケースはたくさんありますよね。

槙田：本当にそうですよね。

澤：先ほどのストーリーテリングの話を受けて言いますと、ちゃんとストーリーが分かっていて、それを正しく伝えるための手段として統計を作っているものはまあまあ信頼していいと思っています。

ですが、全くそういう感じではない統計がたくさんあるにも関わらず、「統計は最強の武器だ」などという人たちが出てくると、私は結構ドキドキしちゃうんです。

槙田：ビッグデータやデータサイエンスといった言葉と一緒に、統計が流行り言葉になっていて、時代がようやく私に追いついてくれてるのはうれしいのですが（笑）、もう片方では、心配でもあるのです。

澤：槙田くんとこの間久しぶりにお話ししたときに、そういう流れで「統計はやばいよね」という話をしていた気がします。この話が、槙田くんが言ってる「統計上の命と顔が見える命」の話に繋がるわけですよね。なるほど。

平均の罠

澤：それから平均って結構危ないですかね？

槙田：はい（ニヤリ）。平均、ヤバいです。一つ例を挙げましょう。

少子高齢化の話題でよく言われる晩婚化について。

女性の平均初婚年齢って２９歳なんですけれど、結婚のピークはこれとは違って２６歳で、３歳も差があります。

それはどういうことかというと、分布を見ればわかります。

澤：確かに分布を確認すれば、左右対称のキレイな山形になっているのかというと、そうではない。

槙田：平均は29歳でも、元の分布でちょうど半分に当たる年齢になるデータの中央値は、それより若い２７歳。そして、最頻値（ピーク）は、さらに下って２６歳になっています。

何をもって「ふつう」と言ってしまうのか。

「ふつう」だなんて、とてもじゃないけど単純に言えるものではなくて。上の話題を取り上げている記事では、これを「平均の罠」と命名し、気を付けるようにと訴えています。

（天野 馨南子 「晩婚化も｢女性の結婚ピークは26歳｣という現実」東洋経済オンライン 2020年12月18日 ・基データは、厚生労働省 人口動態統計）

平均で大喜利を

槙田：平均にまつわるお話は、他にもありまして。

アメリカのプロ野球、メジャーリーグで大谷翔平選手が去年末、ロサンゼルス・ドジャーズに移籍して10年間の超大型契約を結びましたが、その途方もない契約額を使って、「平均」に関するネット大喜利が勃発しました。そのまとめ記事を、ちょっと引用してみましょう。

（『女性自身』編集部 大谷翔平が1人で日本人の平均年収を50円押し上げ！高校同級生は数千万円アップと話題に 2023年12月11日）

数字を使った大喜利には他にもいくつかパターンがあって、例えば、

❝発射台❞になる小さな初期値をテコにして、伸び率を極端に❝盛って❞人目を引く

というストーリーがあります。

ベンチャー企業は初めのうちは小さくて当たり前ですから、うまく成長していった企業なら、顧客数も売上も創業当初に比べたら数字上は何倍にも、数十倍にも見えますよね。

訪日外国人観光客にしても、ひっそりとしていた港町に突然大型クルーズ船が停泊するようになったら、インバウンド需要の倍率はとんでもない数字をたたき出してしまうわけで。

こんな話ばかりで終わるならいいのですけど。

澤： 笑ってばかりもいられない、と。

笑えない数字

槙田：経済を論じたり人々が決断したりする時に、数字だけで語ることは危なっかしかったり罪深いものになったりするのではないでしょうか。

例えば、コロナ禍が急拡大した2020年の春先は、感染を避けるために緊急事態宣言が出て「3密」回避が叫ばれてました。日本経済にとっても大打撃で、その年の4-6月期のGDPは急落しました。

このショックが大きかった分、次の7ｰ9月期はプラス21.4%（速報値）という反動した数字になりました。事実関係で言えば、比較可能な統計のある1980年以来の伸び率としては最大ではありますが、このことだけで奇をてらって報じるようなことはいただけません。

ところで、東京２３区の新築分譲マンションの平均価格が１億円を突破したというニュースも話題になってます。

澤：それってそもそも、販売価格でしたっけ、購入価格でしたっけ。

槙田：さすが澤さん、先ほどから鋭いツッコミです。

報道で騒がれていたのは、供給ベース、販売価格の数字でした。これとは別に、契約ベース、購入価格の数字も、調査主の不動産経済研究所は実は公表しているのですが、マスコミも一緒になって、数字が高く出る販売価格の方ばかり取り上げていました。

澤：実際にはその価格では売れていない、かもしれないわけね。

槙田：そうです。

そして、このマンション価格の「平均」について、先ほどの初婚年齢分布のグラフと同じことが、ここでも起きていないだろうか、ということを知るには、報道記事ではなく、一次情報を見に行かなければなりません。

そこでリリース元である不動産経済研究所のウェブサイトを見にいくのですが、2023年の価格帯別供給戸数の度数分布は、首都圏全体＝1都3県（東京都、神奈川県、埼玉県、千葉県）をまとめたものはあっても、残念なことに、その内訳となる東京23区に限定した度数分布は見当たりませんでした。

澤：そうだったのですか。それは残念というか、むしろ欲求不満になりますねぇ。

槙田：共感してもらえてうれしいです。

餅から米を作る

槙田：ところが、不動産経済研究所は、2023年全体のリリースだけでなく、月単位の平均値のリリースも出してます。それに目を通したら、なんと東京23区だけを抜き出した度数分布もちゃんとあるではないですか。

そこで、面倒くさかったのですが、1月から12月までの資料をダウンロードして、私の手で積み上げてみることを思い立ちました。

PDFファイルの統計表から数字を拾っていく苦行です。人呼んで、これを「 #餅から米 」を作ると言います。 

澤：なるほど・・・。なかなかの趣味ですね（笑）。

槙田： オープンデータ、とっても大事です（泣）。

それでは、12ヶ月分繰り返した成果を、澤さんにご覧いただきましょう。こちらです。

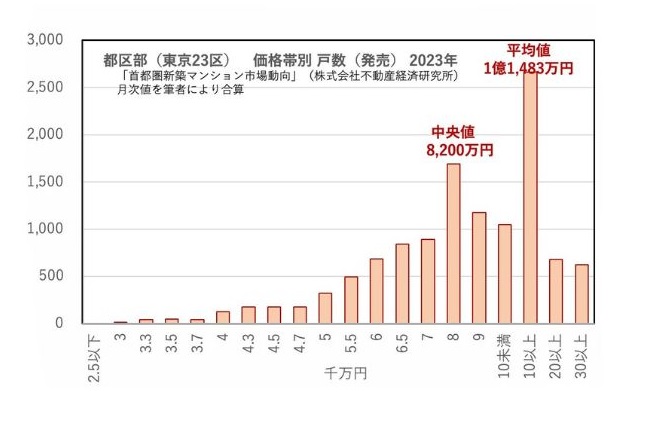
槙田：価格帯の階級幅に注意が必要です。「数百万円」単位が「一千万円」単位になり、1億円を超えると「一億円」単位になっています。

ここまで作ると、この前年とも比較したくなってしまうのが人情です。

そこで、2022年の各月についても同じように12ヶ月積み上げました。それがこちらです。

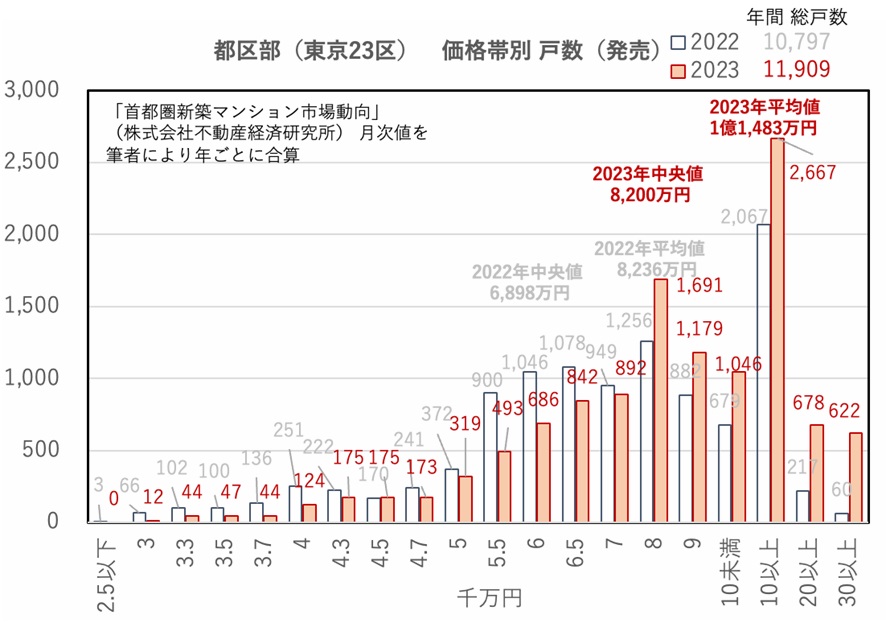
槙田： 2ヶ年のヒストグラムを見比べると、東京23区のマンション価格が高騰ぶりが見えてきます。特に2023年は、1億円を超える物件の供給が怒濤の勢いだった様子がうかがえます。

そして、そのような超高額物件の価格帯では「一億円」単位という階級幅が、ずいぶん大雑把にも感じられてしまいます。

ここで不動産経済研究所のことを思えば、マンション価格の情報を収集・分析・公表されているその筋の老舗であり、このような民間団体の取組には敬意を払うべきと思います。そして、統計の継続性、時系列的な比較可能性のために、階級幅の持たせ方はそう簡単に変えられるものでもないように思えます。

ただ、そのために、2023年になってからの超高額物件の急激な供給量に、階級幅が追いつけていないようにも感じられます。

澤：なるほどね。この階級幅の取り方ではひしゃげた分布になってしまい、高額物件のすそ野の様子がよくわからない。

そして、前年と比較すると、平均の増加幅に対して、中央値の増加幅はそこまで大きいわけではない。

槙田：その中央値なのですが。

中央値８２００万円というリリースを不動産経済研究所が出したのは4月2日でした。それに先立つ平均１億円突破というリリースは１月25日なのですが、この間、２ヶ月以上も時間差があります。

リリースのタイミングをずらして「ため」を設けたは、いったい何のためでしょう。これだけ間が開くのは、ちょっといただけないように思えます。

歪んだ分布の下で数字が高くなってしまう平均が先行し、しかも、節目の「一億円」突破が大きな話題を呼んだ今回の場合、人々の心理に与えられた影響は一層大きなものになってしまったのではないか。

切りのいいその数字。マンションの売り手側にとってセールストークには打ってつけだったでしょうし、物件を探す側の気持ちにとっても必要以上に買い急ぎを迫られたのでは。

日経新聞は4月28日に「新築マンション、夫婦ペアローン拡大」という見出しの記事を打っています。「『背伸び買い』危うさも」という言葉遣いで、家計部門における借金の膨張ぶりを案じています。

マンション価格が高騰傾向にあることは否定のしようがありません。けれども、平均と中央値のリリースが同時のものであったなら、住まいという人生にとって大きな買い物を決断する人にとって、冷静さの度合いは違っていたのでは、と思います。

現実には、「平均価格1億円突破」が先走りして世に出回ったわけですが、そこには「平均の罠」効果があったのではないか、という可能性を否めないのではないでしょうか。

数字を追うな、統計を読め

澤：はじめに私が統計ってあんまり好きじゃない、という話をしたじゃないですか。

正直に物事を見るためにあるのが統計なのに、誤魔化したくてやっているんじゃないか、と思わせる節のものがあるということが、私は気持ちが悪い気がするんだよね。多分、槙田くんの気持ちが悪いもそれに近いのだろうと。

槙田：私の尊敬する職場の先輩が以前書かれた本があるのですが、ここにある通り、その数字はどこから来たものなのかということをちゃんと理解することを意識してほしいです。

佐藤朋彦 2013 「数字を追うな統計を読め」

（※まだまだお話は続きましたが、この後の会話はオフレコとさせていただきます。）

数学経験者の矜持

澤：先ほどもちょっと申し上げたのですが、分布をちゃんと見ましょうよという話とか、平均や中央値、難しく言えば統計量だと思うのですが、それがいったい何を表しているか、ということは、世の中的にはほとんど何も学ばないじゃないですか。

残念ながら数学科にいっても習わないですよね、統計って。統計学部もないし。

本当はちゃんと１個１個のつぶつぶがあって、分布の状態があって、それをどういう風にセグメント化して、という話だし、あとは、全数調査をした方がいい場合もあれば、しても意味がない場合もあるし・・・。

そういうことも含めて余りにも分かっていない状態なのに、統計の話だけはすごく進んでいるように思います。

自分が２０歳くらいの時はノートパソコンが出始めた頃でしたが、今では小学校でも1人1台ノートパソコンを使う時代になりました。RやPythonを使った統計処理を物凄く簡単に分析できるようになっていますよね。

数字を入れると答えが出てくる、有意差が出るからこれでＯＫだな、みたいな。

いやいや、それは出るでしょうよと。

で、出てきた答えに殆ど意味がないのではないか、という検証もなくそれをそのまま論文に書いてしまう人が山ほどいて、そういうところが怖いなと思うんですね。

一方で、槙田くんの意見を聞いてみたいのですが、そういうのが変だ、ということは、数学をやっていたらすぐに気付くじゃないですか。

統計量みたいな情報が集約されている量で分布を語ることが危ないということは、数学をやっている人は直感的に気付くと思うんです。

槙田：はい、そうですね。

澤：それはなぜだと思います？私はこれは数学教育をやるうえで結構大事なことだと思うのですが、意外とみんなが気付いていないのではないかと思っているのですが・・・。

槙田：高飛車な言い方になりますけれど、数学を経験した者であればそのようなことは常識、というか、身体に叩き込まれますよね。

数学というのは、前提となる条件、「公理」が初めにあって、これに基づいて「定義」を組みながら「補定」を積み上げて高みを目指していき、「定理」という美しい眺めにたどり着ける。

そのために、まずは前提を確認したい、この前提があるからこうなりますよ、という訓練の繰り返しじゃないですか。

そういう意味で、数学を経験した人間というのは、前提を確認することは習い性になっていますよね。

澤：そうそう。答えだけでは信用しない。その前提が論理的であるかどうかを常に考えますよね。そしてその証明に穴がないかを全く違う視点で見ようとしますよね。

多分、そういう感覚が、統計を扱う人にはすごく大事なのではないか。いや、統計だけではなくて、仕事をするうえで「本当にこれは正しいんですかね？」という感覚が大事な気がします。

数学をやっている人で統計を扱っている人は、変な伝わり方をしないように一生懸命考えるというか、こう話すとミスリードになっちゃうよな、と考えながら慎重に考えて喋っているような気がするんですけれどね。

槙田：本当に、その繰り返しですよね、数学というのは。

澤：だからこう伝えるとミスリードする人がいるなと思ったら「前提はこうなっています」と明らかにするとか。また、平均値が随分高いように思われる場合はその基になる分布の全体を確認しましょう、とか。数学をやった人にはこうした感覚があるのかなと、今日のお話で改めて思いました。

エピローグ

澤：なかなか面白いですね、あっという間に１時間が経ちましたね。

槙田：そうですね。まだもう少しネタの引き出しから仕込みができるかもしれませんので、もしよかったらまた呼んでください。

澤：どんなことを喋りたいですか？スライドでは「統計を蔵出しで−縦割り組織とオープンデータ」なんて、なかなか刺激的なタイトルが映っていますね。

槙田：これはなにもお役所の話に限ったことではなくて、日本の組織全般について共通する話題ですが、データの相互利用可能性、インターオペラビリティなしにＤＸはできないよね、という「引き出し」です。

澤：今日は１時点の数学というか統計の話が多かったから、次は時間軸をずらした話、みたいなテーマになるかもしれないですね。

今度は事例や方向性を変えてみながら、またＢＡＲこふでをやろうかと思います。またどこかで槙田くんが暇そうなときに、ＢＡＲに来ていただいてお話ができたらと思います。

槙田：わぁ、また来てくれって言ってもらいました！ありがとうございます。では、今日はこれにてお先に失礼します。

澤：ありがとうございます。

はい、これで、お友達も帰られましたので、今日はこのへんで終わりにしたいと思います。

みなさん、１時間にわたりお聞きいただきまして、ありがとうございました。